数据结构与算法
栈
概念
栈是一种遵从后进先出 (LIFO)原则的有序集合。新添加的或待删除的元素都保存在栈的末尾,称作栈顶,另一端叫栈底。
接着我们用js来实现主要的功能点:
- push(element(s)):添加一个(或几个)新元素到栈顶
- pop():移除栈顶的元素,同时返回被移除的元素。
- peek():返回栈顶的元素,不对栈做任何修改(这个方法不会移除栈顶的元素,仅仅返回它)。
- isEmpty():如果栈里没有任何元素就返回true,否则返回false。
- clear():移除栈里的所有元素。
- size():返回栈里的元素个数。
function Stack(){
constructor(){
this.stack = []
}
push(item){
this.stack.push(item)
}
pop(){
return this.stack.pop()
}
peek(){
return this.stack[this.stack.length - 1]
}
size(){
return this.stack.length
}
isEmpty(){
return this.stack.length === 0
}
clear(){
this.stack = []
}
}
场景运用
Leetcode上有效的括号
该题就是一道可以运用栈的思想来解题
/**
* @param {string} s
* @return {boolean}
*/
var isValid = function(s) {
let map = {
'(': -1,
')': 1,
'[': -2,
']': 2,
'{': -3,
'}': 3,
}
let stack = []
for(var v of s){
if(map[v] < 0){
stack.push(map[v])
}else{
let n = stack.pop()
if(n + map[v] !=0) return false
}
}
if(stack.length > 0) return false
return true
};
队列
概念
队列是遵循先进先出(FIFO)原则的一组有序的项。队列在尾部添加新元素,并从顶部移除元素。最新添加的元素必须排在队列的末尾。
在现实中,最常见的队列的例子就是排队。
用js来实现主要的功能点:
- enqueue(element(s)):向队列尾部添加一个或多个新的项
- dqueue():移除队列的第一项,并返回被移除的元素
- front():返回队列中第一个元素。。队列不做任何变动
- isEmpty():如果队列中不包含任何元素,返回true,否则返回false。
- size():返回队列包含的元素个数
class Queue(){
constructor(){
this.queue = []
}
enqueue(item){
this.queue.push(item)
}
dqueue(){
return this.queue.shift()
}
front(){
return this.queue[0]
}
isEmpty(){
return this.queue.length === 0
}
size(){
return this.queue.length
}
}
队列的扩展还有 最小优先队列、最大优先队列、循环队列等
最小优先队列,是把优先级的值较小的元素被放置在队列最前面
最大优先队列,是把优先级的值较大的元素被放置在队列最前面
链表
概念
链表是一个线性结构,同时也是一个天然的递归结构。链表结构可以充分利用计算机内存空间,实现灵活的内存动态管理。但是链表失去了数组随机读取的优点,同时链表由于增加了结点的指针域,空间开销比较大。
js 实现
class Node{
constructor(value,next){
this.value = value;
this.next = next
}
}
class LinkedList{
constructor(){
this.length = 0
this.header = null
}
checkIndex(index) { // 判断是否越界
if (index < 0 || index > this.length) throw Error('Index error')
}
find(node = this.header,index,currentIndex = 0 ){ // 查找对应位置的节点
if(index == cunrrentIndex ) return node
return this.find(node.next,index,currentIndex + 1)
}
addNode(element,index){
this.checkIndex(index)
if(index == 0){
this.header = new Node(element,null);
return
}
let currentNode = this.find(index)
currentNode.next = new Node(v,currentNode.next) // 变更点前位置node.next的值 并将新node的next 变更为之前的值
this.length ++
}
remove(index){ // 从列表中移除一项。
this.check(index)
let currentNode = this.find(index)
let node = currentNode.next
currentNode.next = node.next
node.next = null
this.length --;
}
}
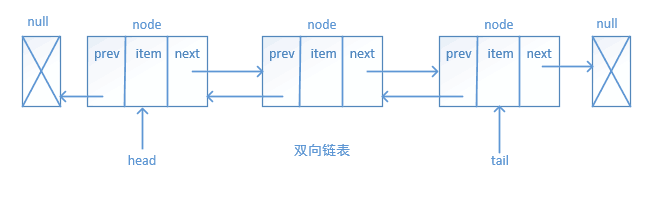
双向链表
双向链表和普通链表的区别在于,在链表中, 一个节点只有链向下一个节点的链接,而在双向链表中,链接是双向的:一个链向下一个元素, 另一个链向前一个元素
class DoublyNode extends Node {
constructor(value,perv,next){
super(value,next)
this.next = next
}
}
class DoublyLinkedList{
constructor(){
this.length = 0;
this.header = null
this.tail = null // 尾指针
}
checkIndex(index) { // 判断是否越界
if (index < 0 || index > this.length) throw Error('Index error')
}
find(node = this.header,index,currentIndex = 0 ){ // 查找对应位置的节点
if(index == cunrrentIndex ) return node
return this.find(node.next,index,currentIndex + 1)
}
addNode(element,index){
this.checkIndex(index)
let currentNode = this.find(index)
let newNode = new DoublyNode(v,currentNode,currentNode.next)
currentNode.next.perv = newNode
currentNode.next = newNode
this.length ++
}
remove(index){ // 从列表中移除一项。
this.check(index)
let currentNode = this.find(index)
currentNode.next.perv = currentNode.perv
currentNode.perv.next = currentNode.next
this.length --;
}
}
树
一个树结构包含一系列存在父子关系的节点。每个节点都有一个父节点(除了顶部的第一个节点)以及零个或多个子节点。位于树顶部的节点叫作根节点,它没有父节点。
节点的一个属性是深度,节点的深度取决于它的祖先节点的数量;树的高度取决于所有节点深度的最大值。
二叉树和二叉搜索树
二叉树中的节点最多只能有两个子节点:一个是左侧子节点,另一个是右侧子节点。
二叉搜索树(BST)是二叉树的一种,但是它只允许你在左侧节点存储(比父节点)小的值, 在右侧节点存储(比父节点)大(或者等于)的值。
js来实现二叉搜索树一些基本功能:
- insertNode(key):向树中插入一个新的键。
- search(key):在树中查找一个键,如果节点存在,则返回true;如果不存在,则返回false。
- remove(key):从树中移除某个键。
- deep() 树的深度
class TreeNode{
constructor(key){
this.key = key;
this.left = null;
this.right = null;
}
}
class BinarySearchTree{
constructor(){
this.root = null
}
// 插入节点
insertNode(key,partenNode){
let node = new TreeNode(key)
if(!this.root){
this.root = node
}else{
if(partenNode.key > key){
if(!partenNode.left){
partenNode.left = node
}else{
insertNode(key, partenNode.left)
}
}else{
if(!partenNode.right){
partenNode.right = node
}else{
insertNode(key, partenNode.right)
}
}
}
}
search(key,node){
let res = false
if(!node){
return false
}
if(node.key > key && node.left){
res = this.search(key,node.left)
}
if(node.key < key && node.right){
res = this.search(key,node.right)
}
if( node.key === key){
res = true
}
return res
}
removeNode(key,node){
if(!node){
return
}
if(key < node.key){
removeNode(key,node.left)
}else if(key> node.key){
removeNode(key,node.right)
}else{
if(node.left == null && node.right==null){
node = null
return node
}
if(node.left === null){
node = node.right
return node
}
if(node.right === null){
node = node.left
return node
}
var _node = findMinNode(node.right) // 查找最小的子节点
node.key = _node.key
node.right = removeNode(_node.key,node.right)
return node
}
}
// 树的深度
deep(){
if(!this.root){
return 0
}
return Math.max(deep(this.root.left),deep(this.root.right)) + 1
}
}
树的遍历
树的遍历具有3种方式。
先序遍历 表示先访问根节点,然后访问左节点,最后访问右节点。
中序遍历 表示先访问左节点,然后访问根节点,最后访问右节点。
后序遍历 后序遍历表示先访问左节点,然后访问右节点,最后访问根节点。
三者的差别就是在于根节点在第一个访问。
先序遍历
preOrderTraverse(node,callback){
if(node){
callback(node.key)
preOrderTraverse(this.left,callback)
preOrderTraverse(this.right,callback)
}
}
中序遍历
inOrderTraverse(node){
if(node){
inOrderTraverse(this.left)
callback(node.key)
inOrderTraversse(this.right)
}
}
后序遍历
postOrderTraverse(node){
if(node){
postOrderTraverse(this.left)
postOrderTraverse(this.right)
callback(node.key)
}
}
平衡二叉树 AVL
图
算法时间复杂度
如何衡量算法的效率?通常是用资源,例如CPU(时间)占用、内存占用、硬盘占用和网络占用。当讨论大O表示法时,一般考虑的是CPU(时间)占用。
通常使用最差的时间复杂度来衡量一个算法的好坏。
常数时间复杂度O(1) 代表这个操作和数据量没有关系,是一个固定时间的操作,比如说四则运算。
时间复杂度是O(n) 举个例子来说 遍历一个数组查找一个数,现在假设这个数组长度为10,那最坏的结果就是遍历10次,这个数在最末尾。那么如果数组无限大,长度为n表示,那么最坏的情况是不是就是遍历n次,从而得出时间复杂度O(n)
时间复杂度O(n2) 典型的例子就是冒泡 是不是2层循环。
参考链接